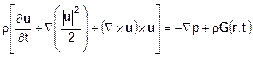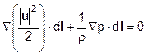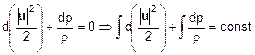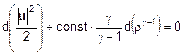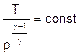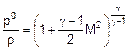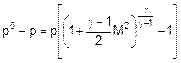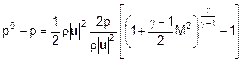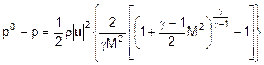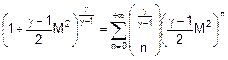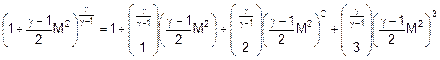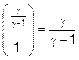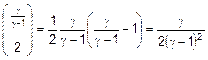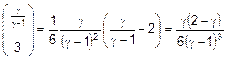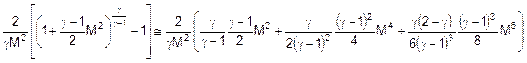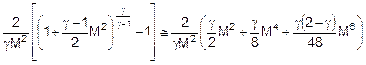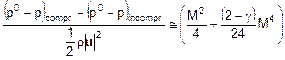|
· · Fluidodinamica e Aerodinamica · Aerodinamica · · SOGLIA DEL REGIME DI MOTO INCOMPRIMIBILE · Valerio
D'Alessandro · · INTRODUZIONE · Equazioni
del moto · Comprimibilità
vs. Incomprimibilità · BIBLIOGRAFIA
· · · ·
·
· INTRODUZIONE
I fluidi presenti in natura sono tutti viscosi e
comprimibili. Le equazioni che regolano le condizioni dinamiche dei fluidi
viscosi e comprimibili risultano, purtroppo, di difficile applicazione e
manipolazione al fine di risolvere problemi di interesse ingegneristico in
quanto le equazioni di conservazione della massa, della quantità di moto e
dell’energia sono più complesse di quanto appaiono: sono non lineari,
accoppiate e difficili da risolvere, è difficile, inoltre, provare con i
metodi matematici esistenti l’esistenza di una soluzione unica per
particolari condizioni al contorno. Solo in particolari casi – flussi completamente
sviluppati in geometrie semplici – è possibile ottenere una soluzione
analitica delle equazioni di Navier – Stokes e questi flussi sono importanti
per lo studio dei fondamenti della fluidodinamica ma sono del tutto
irrilevanti dal punto di vista pratico. In determinate condizioni di flusso, però, è possibile
semplificare le equazioni in quanto alcuni termini in esse presenti sono poco
importanti o trascurabili rispetto ad altri e, nonostante ciò, è possibile
che perfino le equazioni semplificate risulti anch’esse molto complesse e non
ammettano soluzione analitica ed è quindi necessario introdurre metodi
numerici. In questa breve trattazione si vuole descrivere un
criterio per trascurare la comprimibilità del fluido in determinate
condizioni di moto. Equazioni
del moto
Come è noto le equazioni che regolano lo stato di
dinamico di un fluido (in condizioni di viscosità indipendente dalla temperatura,
modello termodinamico: gas perfetto, modello reologico: fluido newtoniano non
micropolare; tipicamente acqua e aria) sono:
A partire dall’equazione della quantità di moto scritta
in forma di Lagrange nell’ipotesi di fluido non viscoso si ottiene:
si arriva, quindi, alla seguente espressione
(considerando il moto stazionario, St>>1, e trascurando le forze di
massa):
se il moto è irrotazionale (Ñxu=0) si ottiene:
che è equivalente a:
l’integrale in cui compare il termine barico può essere
calcolato solo a partire da ipotesi ben precise sulla relazione fra pressione
e densità. Nell’ ipotesi di fluido incomprimibile si ottiene:
che è la celebre espressione del Teorema di Bernuolli.
Se, invece, si considera il fluido comprimile allora la pressione e la densità del fluido saranno
legate dalla relazione:
purchè il moto sia omoentropico (entropia della
corrente imperturbata uniforme, assenza di scambi termici, dissipazioni viscose
e, ovviamente, di onde d’urto). Se la si differenzia si ottiene:
cioè:
la relazione sopra integrata porta a scrivere:
con “a” velocità sonica locale. Se la particolare
particella fluida viene arrestata dalla sua condizione dinamica in modo
isoentropico si può scrivere:
con a0 velocità del suono di ristagno. Sfruttando
la relazione di Laplace a2=gRT si può quindi scrivere (in seguito a qualche piccolo
passaggio algebrico omesso):
con:
numero di Mach. Dalla (1), sfruttando la relazione
si arriva all’importante relazione:
la corrispondente relazione della (2) in regime incomprimibile
è:
(è scontato dire che nell’ipotesi di flusso
irrotazionale il teorema di Bernoulli vale in senso forte cioè fra una
qualsiasi coppia di punti del campo di moto, invece, nell’ipotesi di fluido
non viscoso in moto rotazionale, il teorema di Bernoulli vale in senso debole
cioè fra una coppia di punti appartenenti ad una medesima linea di corrente.) Comprimibilità vs. Incomprimibilità L’idea è quella stimare l’errore che si commette nel calcolo
della pressione del fluido considerando il fluido incomprimibile piuttosto
che comprimibile a partire dai binomi bernoulliani. L’andamento della
pressione è stimato, lecitamente, in condizioni irrotazionali in quanto nei
flussi in cui esiste lo strato limite (e lo strato limite non è separato) la
distribuzione di pressione alla parete è determinata dal moto a potenziale
esterno allo strato limite. Da (2) si deduce che:
da cui:
dalla quale:
il termine fra parentesi
graffe stima quantitativamente l’errore che si commette nel considerare il
fluido incomprimibile piuttosto che comprimibile (in altre parole lo si
potrebbe definire come lo scostamento dal “comportamento incomprimibile” del
fluido). Se il fattore, dipendente dal numero di Mach, induce un
errore inferiore al 5% allora l’approssimazione di fluido incomprimibile è
del tutto lecita. Il lavoro che bisogna fare, in definitiva, consiste nello
stimare l’intervallo di numero di Mach che produce errori accettabili nel
trascurare la comprimibilità del fluido. Essendo g=1,4 allora (g-1)/2<1, nell’ipotesi di M<1
(moto subsonico) è possibile fare uso del seguente sviluppo in serie
binomiale:
trascurando i termini di ordine superiore al terzo
ordine si ha:
con:
ricordando che:
Facendo le opportune sostituzioni si arriva a scrivere
che:
la quale si può essere ridotta a (con passaggi
algebrici banalissimi):
tornando a (3) si ottiene:
quindi:
In definitiva se vale la disuguaglianza:
l’approssimazione di fluido incomprimibile è sensata.
Dalla soluzione di (4) si riesce, quindi, ad individuare il range utile di
numeri di Mach in cui è lecito considerare trascurabile la comprimibilità del
fluido in esame. Se si riordina (4) si ottiene:
il trinomio al primo membro è chiaramente di secondo
grado in M2 e presenta le seguenti radici:
la soluzione di (5) per g=1,4 è M2<0,117 cioè M<0,342. Il risultato raggiunto significa che numeri di Mach inferiori
a 0,342 l’errore che si commette nel trascurare la comprimibilità del fluido
in esame è in inferiore al 5% (che dal punto di vista ingegneristico è del
tutto accettabile). Convenzionalmente la soglia che determina il regime di
moto incomprimibile è individuato da numeri di Mach inferiori a 0.3. Bibbliografia
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ingegneriaaerospaziale.net -
Tutti i Diritti Riservati |